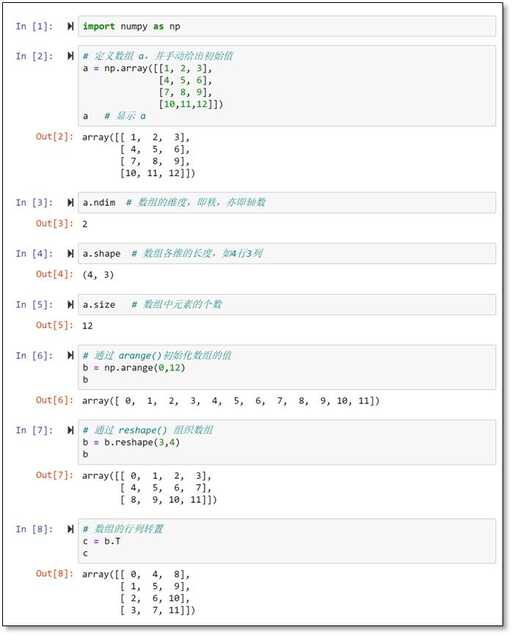
j矩陣乘法特點？

使用二維數(shù)組作為矩陣的存儲結(jié)構(gòu)，根據(jù)轉(zhuǎn)置矩陣的特點，很容易得到轉(zhuǎn)置矩陣。矩陣相乘的特點：

（1）當(dāng)矩陣A的列數(shù)等于矩陣B的行數(shù)時，A與B才可以相乘。

（2）乘積C的第m行第n列的元素等于矩陣A的第m行的元素與矩陣B的第n列對應(yīng)元素乘積之和。

（3）矩陣C的行數(shù)等于矩陣A的行數(shù)，C的列數(shù)等于B的列數(shù)。

兩矩陣轉(zhuǎn)置后相乘與相乘后轉(zhuǎn)置不相等。證明如下：

把矩陣A的行換成相應(yīng)的列，得到的新矩陣稱為A的轉(zhuǎn)置矩陣，記作A^T或A’。

根據(jù)基本性質(zhì)(A±B)'=A'±B'；(A×B)'=

B'×A'；(A')'=A；(λA')'=λA；det(A')=det(A)。

所以轉(zhuǎn)置后相乘和相乘后轉(zhuǎn)置，也就是（A'×B'）和A'×B'一般是不相等的。

必須是轉(zhuǎn)置后相乘和相乘后轉(zhuǎn)置兩個之間的左右乘位置對調(diào)才相等；即（A'×B'）和B'×A'才是相等的。而B'×A'和A'×B'一般是不相等的，矩陣乘法一般不滿足乘法交換律。