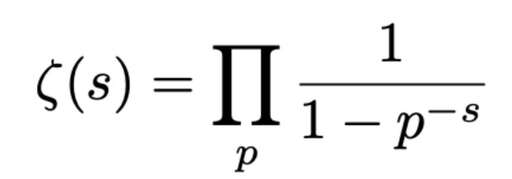elgamal算法例題？

ElGamal算法是一種常見加密算法, 與Diffie-Hellman算法有密切關聯。

該算法安全性依賴于計算有限域上離散對數難題：求解離散對數(目前)是困難的,其逆運算指數運算簡單。

算法思路:

假設有2個用戶Alice 和 Bob，Bob欲使用ElGamal加密算法向Alice發送信息。對于Alice,首先要選擇一個素數q, α是素數q的本原根。 [本原根的概念對應模q乘法群(需循環群)中的生成元。

Alice產生一個

? ,

? ∈(1, q - 1)

計算

? =

? mod q

A的私鑰為

? , 公鑰為 {q, α,

? }

公鑰存在于某個可信公開中心目錄,任何用戶都可訪問對于Bob, 首先去上述中心目錄訪問得Alice的公鑰 {q, α,

? }

然后將自己欲發送的明文M, (M ∈ [1, q - 1]）洗干凈備好。

選一個隨機整數k, k ∈ [1, q - 1]

計算可解密自己密文的秘鑰 PrivateK =

? mod q

C1 =

? mod q , C2 = PrivateK * M mod q

明文對發送給Alice

Alice收到明文對：

PrivateK =

? mod

M = C2 *

? mod q

到這里..發現算法大多就是一些乘法,求冪之類的運算。剩下個關鍵內容就是如何尋找素數p的本原根，或者說如何找有限域GF(p)中的生成元。

我們在群這個概念里討論。

p是素數，令Zp = {1, 2, 3, ..., p - 1},因為考慮乘法，去掉了0元素。

2個定理：

Euler定理：設P和a是互素的兩個整數，則有aφ(p)＝1 mod p

拉格朗日定理: 設 G 是有限群， H 是 G 的子群,|H| 整除 |G

回顧這樣2個概念：設G是群, a∈G, 使得等式ak = e成立的最小整數k稱為元素a的階。而群的階是指該群中的元素個數。值得留意的是，以某個生成元去生成某個子群，該子群的階就是該元素的階(當然了）。

因Zp中所有元素與p互素,由歐拉定理，Zp中所有元素的階不超過p-1,(因為群的階φ(p)是p-1,而至少有aφ(p)＝1 mod p)。

對于Zp中的任一元素，以該元素為生成元形成的一個循環群，設為S(群S的階在數值上即該元素的階)，根據群的封閉性可知S必然為Zp的子群，根據拉格朗日定理，可知Zp的元素的階必然是|Zp| (即p-1)的因子。

于是可以得到這樣一個結論：若有這樣一個元素a，其階為Ka, Ka是p-1的平凡因子(即因子1 或者因子p-1), 那么a或者是單位元，或者是生成元。 又知Zp的單位元是1，那么根據單位元的唯一性，可知若a非1，則a必為生成元。問題在于，p-1的因子可能很多，我們還不是得一個個去找到階是p-1的平凡因子的元素？

為此，我們構造一種特殊的素數，使得p-1的因子數量很少。取p - 1 = 2 * Q ，其中p是素數，Q也是素數。 因為Q是素數，因子僅1， Q。所以p - 1的因子只有 {1, 2, Q, p - 1}四個。

到此已經非常明朗，我們找到滿足上述條件的素數p，然后在Zp中尋找這樣一個元素a，a的階非2，非Q，即a^2 mod p != 1 && a^Q mod p != 1，若a又非單位元1，那么a必然是生成元

留意Zp未必一定有生成元, 若1 到 (p - 1)經上述檢驗都不滿足, 考慮另取一個素數p。至于代碼實現上出現的問題：若mpz_probab_prime_p(tmp.mt, 6) == 1 改為 mpz_probab_prime_p(tmp.mt, 6) == 2，p一旦較大，程序運行速度很慢。取2為真素數檢驗，速度很慢，1為概率素數檢驗，速度快